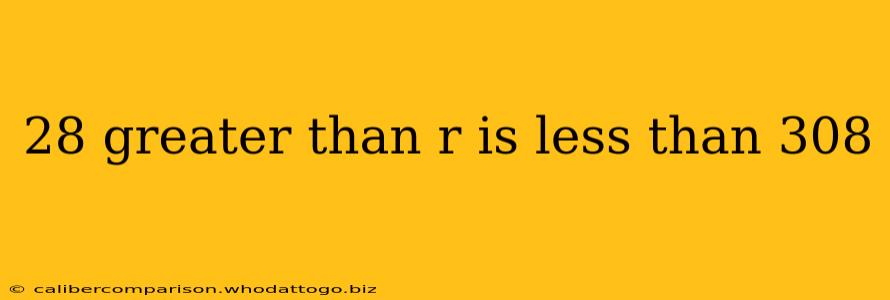Decoding the Inequality: 28 < r < 308
This seemingly simple inequality, 28 < r < 308, holds a significant amount of information for those working with numerical ranges, data analysis, or even basic algebra. Let's break down what it means and explore its implications.
Understanding the Inequality
The statement 28 < r < 308 signifies that the variable 'r' represents a value that falls between 28 and 308. Crucially, it's strictly between these two numbers; 'r' cannot be equal to 28 or 308. This is indicated by the use of the "less than" symbol (<) on both sides.
Practical Applications
This type of inequality pops up in numerous scenarios:
-
Data Ranges: Imagine analyzing a dataset of temperatures. If all recorded temperatures fall within the range of 28° to 308° (perhaps Celsius or Fahrenheit), then this inequality accurately reflects the possible temperature values (r).
-
Programming and Algorithms: In computer programming, constraints like this might be used to define acceptable input values or to set boundaries within a loop or function. For example, a program processing image data might only accept values for pixel brightness (represented by 'r') within this specific range.
-
Mathematical Modeling: Many mathematical models use inequalities to represent real-world constraints. For instance, in supply chain management, 'r' might represent the quantity of a certain product that is available, limited by both minimum and maximum production levels.
-
Statistics: Confidence intervals often rely on inequalities to define a range of plausible values for a population parameter. For instance, a 95% confidence interval for the average height of a population could be expressed similarly, indicating the plausible range for the average height.
Solving Problems Involving This Inequality
Solving problems involving this type of inequality typically involves determining if a given value falls within the specified range or finding values that satisfy the inequality.
Example: Is r = 150 a valid solution?
Yes, because 28 < 150 < 308.
Example: Is r = 308 a valid solution?
No, because the inequality states that r must be less than 308.
Visualizing the Inequality
It's often helpful to visualize this inequality on a number line:
--------------------------------------------------
28 308
<----------------------------------------------->
r falls within this range
This visual representation clearly shows the range of possible values for 'r'.
Conclusion
The inequality 28 < r < 308 concisely defines a specific range of numerical values. Understanding its meaning is crucial for anyone working with data, algorithms, mathematical models, or statistical analysis. Its simple form belies its broad applicability across numerous fields. Remember the key: 'r' must be strictly greater than 28 and strictly less than 308.